Regreso después de unas vacacaciones durante las cuales la nostalgia me hizo regresar a la solución de ejercicios de las Olimpiadas Internacionales de Matemáticas. Esta vez les narraré cómo obtuve con ayuda de Eukleides la figura de uno de los problemas de geometría que resolví. La necesitaba para publicar la demostración en un nuevo blog de Soluciones de Olimpiadas, donde trataré de documentar mis experiencias en la lucha constante que ha representado la resolución de estos ejercicios tan complejos. ¡Ojalá hubiéramos tenido una herramienta como esa en mis tiempos! Espero que les sea útil a ustedes también. Me siento satisfecho puesto a que hace más de siete años que no intentaba resolverlos, así que todavía estoy en forma :o). Usted puede suscribirse a este blog si desea estar al tanto de otros temas igual de interesantes. Si lo desea también puede recibir automáticamente las respuestas a los ejercicios que se irán publicando en el nuevo blog de Soluciones de Olimpiadas. Si Usted desea también puede solicitar permisos para publicar sus propias soluciones, o artículos relacionados con estos eventos.
¿Qué es Eukleides?
Existen varias alternativas para lograr que una computadora dibuje figuras geométricas en el plano. LaTeX es una de ellas. Sin embargo, en gran parte de los casos hay que emplear herramientas diseñadas desde el punto de vista del funcionamiento interno de la computadora. En otros casos hay que especificar hasta el más mínimo detalle para obtener una figura medianamente comprensible. Todo esto dificulta el aprendizaje y la rápida familiarización de los usuarios con la herramienta, puesto a que se impone una nueva forma de pensar y a veces se necesita hasta realizar cálculos no siempre evidentes.
Eukleides es una herramienta genial que interpreta un lenguaje descriptivo para obtener representaciones de figuras de la geometría euclideana. Sus características permiten que se pueda obtener una figura conociendo solamente los conceptos matemáticos y las relaciones entre los puntos y las curvas que se mencionan en el ejercicio en cuestión. Resulta asombroso que el enunciado del problema se pueda traducir casi directamente para obtener la descripción de la figura. Utilicemos el mismo problema de geometría que resolví para ilustrar lo que estoy diciendo. Su enunciado es el siguiente :
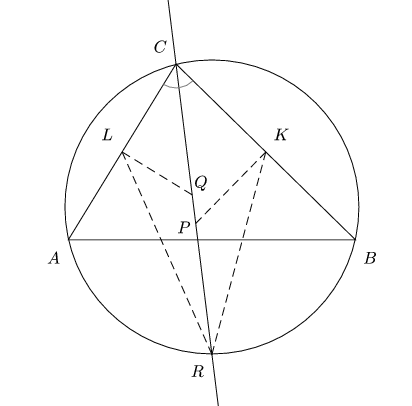
Problema 4 - IMO 2007 (Vietnam). En un triángulo ABC la bisectriz del ángulo BCA y la circunferencia circunscrita al triángulo se cortan en R (R != C). Dicha recta corta a la mediatriz de BC en P y a la mediatriz de AC en Q . El punto medio de BC es K y el punto medio de AC es L . Demostrar que los triángulos RPK y RQL tienen áreas iguales.
A continuación representaré las condiciones del problema (resaltadas en negritas ;o) en el órden que van apareciendo en el enunciado de problema. Solo tengan en cuenta que utilizo la sintaxis de la versión 1.0.3 de eukleides (después explico más al respecto ;o)
A B C triangle
l = bisector(B, C, A)
c = circle(A, B, C)
C R intersection(l, c)
P = intersection(l, perpendicular(segment(B, C), midpoint(segment(B, C)) ))
Q = intersection(l, perpendicular(segment(A, C), midpoint(segment(A, C)) ))
K = midpoint(segment(B, C))
L = midpoint(segment(A, C))
draw(A, B, C)
draw(l)
draw(c)
draw(segment(K, P), dashed)
draw(segment(L, Q), dashed)
draw("$A$", A, -130:)
draw("$B$", B, -50:)
draw("$C$", C, 130:)
draw("$P$", P, 0.1, -160:)
draw("$Q$", Q, 0.1, 50:)
draw("$R$", R, -130:)
draw("$K$", K, 50:)
draw("$L$", L, 130:)
color(gray)
mark(A, C, R)
mark(B, C, R)
Esto es todo lo que se necesita. Como se puede apreciar el lenguaje es declarativo y resulta increíble la similitud con el enunciado del problema. También hay que resaltar que hay comandos específicos para dibujar y para denotar los puntos y rectas que aparecen en la figura. Con ellos se pueden obtener distintos estilos y formas.
Para obtener la figura incluimos en texto anterior en el fichero imo2k7pb4.euk y luego instalamos eukleides y sus dependencias (Eukleides utiliza las extensiones PSTricks de LaTeX). En Debian o Ubuntu solo está empaquetada la la versión 1.0.3 de eukleides, pero la la versión 1.5.4 de eukleides cubre las mismas necesidades con un lenguaje más expresivo. Sin embargo es posible encontrar la versión 1.5.4 empaquetada en sid, por lo que quizás pronto la tendremos en los repositorios. La instalación se haría de la siguiente manera :
$ sudo apt-get install eukleides ; XXX dependencias
Después se utiliza el comando euk2edit y se especifica el formato de salida que se desea obtener (en este caso un fichero PostScript)
$ euk2edit imo2k7pb4.euk ps
El fichero imo2k7pb4.ps contiene ahora la figura en el formato deseado. Para conocer todos los formatos que se pueden obtener, basta con leer la salida del comando
$ pstoedit -help
Conclusiones
La herramienta también permite la traducción de los comandos a varios idiomas. El fichero anterior podría ser escrito también en español (si hubiera una traducción ;o) de esta forma
A B C triangulo
l = bisectriz(B, C, A)
c = circulo(A, B, C)
C R interseccion(l, c)
P = interseccion(l, perpendicular(segmento(B, C), puntomedio(segmento(B, C)) ))
Q = interseccion(l, perpendicular(segmento(A, C), puntomedio(segmento(A, C)) ))
K = puntomedio(segmento(B, C))
L = puntomedio(segmento(A, C))
dibuja(A, B, C)
dibuja(l)
dibuja(c)
dibuja(segmento(K, P), discontinuo)
dibuja(segmento(L, Q), discontinuo)
dibuja("$A$", A, -130:)
dibuja("$B$", B, -50:)
dibuja("$C$", C, 130:)
dibuja("$P$", P, 0.1, -160:)
dibuja("$Q$", Q, 0.1, 50:)
dibuja("$R$", R, -130:)
dibuja("$K$", K, 50:)
dibuja("$L$", L, 130:)
color(gris)
resalta(A, C, R)
resalta(B, C, R)
Si consideramos que existe una herramienta visual llamada xeukleides, entonces ¡hasta un niño podría hacer esto y obtener sus figuras! . Espero que les haya gustado este artículo. Suscríbase a este blog si desea continuar este viaje para descubrir las bondades de los diferentes software libres. No olvide que si Usted desea también puede solicitar permisos para publicar sus propias demostraciones en el blog de Soluciones de Olimpiadas, o artículos relacionados con estos eventos. La invitación está hecha para recibir automáticamente las respuestas a los ejercicios que se irán publicando allí.