La cara oculta de Fibonacci (en Python)

Este artículo puede ser muy útil para que todos aquellos que se aferran a los resultados y conclusiones teóricas pues sean más cuidadosos al analizar sus resultados. Los números de Fibonacci nos revelerán las grandes distancias que pueden existir entre la teoría y la práctica. Esta famosa sucesión, que en sus orígenes fue útil para cuantificar la reproducción de los conejos, todavía sigue sorprendiendo a los teóricos de las matemáticas y otras ramas como las ciencias de la computación. En este caso revelaremos el secreto que se esconde tras un algoritmo aparentemente simple. No hay trucos, ni engaños de ningún tipo. Continúe leyendo hasta el final y seguro que se sorprenderá. Este es el primer espacio que dedico a analizar algoritmos útiles y sus diversas implementaciones. Si le interesa este tema o cualquier otro que se trate en este blog, Usted puede suscribire para recibir los próximos artículos. Le comento que pronto mencionaré sucesos realmente polémicos y candentes. Le invito también a que siga este blog, para así recorrer juntos el camino que nos lleve a todos a la comprensión de las tecnologías actuales y sus fundamentos.

Algoritmo simple para generar la serie

Seguramente todos conocen un algoritmo sencillo y eficiente (e.g. O(n)) para calcular los números de Fibonacci. A continuación les muestro su implementación en Python :

def Fibonacci(n):
  fn = f1 = f2 = 1
  for x in xrange(2, n):
    fn = f1 + f2
    f2, f1 = f1, fn
  return fn

if __name__ == '__main__' :
  from time import time
  
  def measure(n) :
    st = time()
    Fibonacci(n)
    return time() - st
  
  for data in ((x, sum(measure(x) for _ in xrange(10)) / 10) for x in xrange(25000)):
    print "%s,%s" % data

Sencillo, ¿verdad? Es muy fácil darse cuenta de que el número de sumas que se necesitan es proporcional al valor del argumento n. Por tanto a nadie dudaría al afirmar que esta implementación es muy eficiente y del órden O(n). Pero sería bueno preguntarse : ¿es esto lo que sucede realmente cuándo se ejecuta?

El ser tiene memoria ontológica en la praxis

Verifiquemos si el tiempo de ejecución de este algoritmo es realmente lineal. En este caso deberíamos obtener valores con pequeñas desviaciones alrededor de una recta. Las variaciones pueden estar dadas por la intervención del planificador de procesos del sistema operativo, la atención a interrupciones y otros muchos factores que realmente están fuera de nuestro control y pueden variar de un momento a otro, o de una computadora a otra. Grafiquemos los tiempos de ejecución para números menores que 46. Cada valor mostrado es el promedio los tiempos reportados por el comando que aparece a continuación al realizar 10 ensayos con el mismo valor de n :

$ python work/temp/fib/fib.py > work/temp/fib/fib.csv

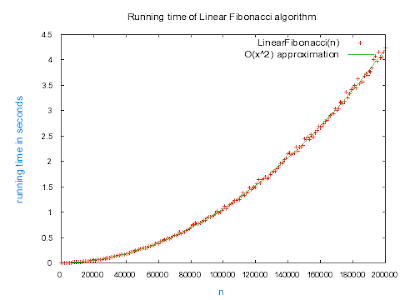
¿Cuáles son los resultados? Bueno realmente no hay nada más parecido a una recta. En este momento Usted se preguntará ¿cuál es el misterio? , ¿me están tomando el pelo?, ¿esto es una broma?, ¿me están hacendo perder mi tiempo?. No se deje llevar por las apariencias. Veamos otro gráfico obtenido al repetir los ensayos con los números enteros menores que 25,000 (tomados a intervalos de 50 para que los datos no sean tan voluminosos ;o).

¡No es posible! El incremento en este caso no es para nada lineal, sino que la curva parece una parábola. Incluso si se trata de realizar un ajuste con una función cuadrática la coincidencia se hace muy evidente. ¿Cómo es posible que se comporte con este crecimiento cuadrático (i.e. O(n²))?

Revelando el secreto

La causa fundamental por la que en este caso los resultados teóricos difieren tan significativamente de los prácticos es que en el primer caso se asumió que durante la ejecución todas las sumas se ejecutaban en un tiempo constante, pero esto no es así cuando se lleva a cabo el proceso en un ordenador real. El hecho de que para números pequeños la linealidad se mantiene, nos da una pista muy importante para buscar la raíz del problema. ¿Todavía no se les ocurre nada? Todos aquellos que mencionaron la aritmética de los números enteros grandes definitivamente acertaron.

A medida que se van computando nuevos números de la sucesión, los valores se van haciendo tan grandes, que exceden los 32 bits (y eventualmente también los 64 bits) de la arquitectura de base. Por tal razón hay que apelar al tipo long. Claro que el lenguaje es consistente y todo esto resulta transparente para el programador. Pero, al mismo tiempo el costo para calcular cada suma se va haciendo proporcional a la longitud del número de Fibonacci previo. La adición de dos números grandes de longitud O(n) es un algoritmo lineal (i.e. O(n)).

La demostración matemática

A continuación les presento un análisis que explica la baja eficiencia del algoritmo mencionado, cuando se ejecuta en una PC real. Se considera el procesamiento adicional y solapado realizado por la librería bigint.

En cada iteración i se realiza un número de operaciones del órden O(número de dígitos de fib_N) = O(digits(fib_N)). Por tanto es necesario sumar todos estos valores para cada número (i.e. valor de i) entre 1 y n:

Pero, ¿cuál es el número de dígitos del enésimo número de Fibonacci? Como punto de partida tomaremos la fórmula de Binet. La misma enuncia que el enésimo número de Fibonacci puede ser expresado por calculado utilizando la fórmula siguiente :

El número de dígitos de un número se puede calcular hallando la parte entera del valor log ₁₀ (number) + 1. Por tanto la cifra que buscamos es nada más y nada menos :

Al sumar todos los costos en los que se incurre para el valor final, se obtiene la siguiente expression:

Se puede observar cómo el tiempo de ejecución de este algoritmo "lineal" realmente resulta ser cuadrático, considerando que cada suma se ejecuta en un tiempo proporcional a la cantidad de dígitos de los números de Fibonacci involucrados.

Conclusiones

Los métodos y resultados teóricos son de un valor tremendo para las matemáticas y las ciencias de la computación en general. La belleza y al mismo tiempo complejidad de las demostraciones es una fuente de sorpresa. Su comprensión desarrolla nuestra capacidad de razocinio y otras habilidades que nos permitirían comprender más a fondo el mundo que nos rodea. Sin embargo, la realidad suele ser mucho más rica. Por tanto es de vital importancia comprender y validar las hipótesis antes de emitir un juicio definitivo, y aplicar los teoremas y corolarios con mucho cuidado.

Si desea participar en este recorrido que realizaré para ilustrar aspectos interesantes de varios algoritmos famosos, le invito a estar al tanto de los próximos artículos. Pero estos no son los únicos temas que se tratan aquí en el blog de Simelo. Le invito también a que siga este blog. ¡ Seguro que no se arrepentirá !